ASP 460 2.0 Data VisualizationDr Thiyanga TalagalaPrincipal Component Analysis1 / 26

PCA

Finding low-dimensional combinations (or projections) of high dimensional data that capture most of the variability in the original data.
Objective: Take $P$ variables $X_{1}, X_{2}, X_{3}, . . . X_{p}$ and find combinations of these to produce variables (components) $Z_{1}, Z_{2} . . . Z_{p}$ that are uncorrelated.

Number of PCs = Number of variables in the original data.

The components are ordered so that $Z_{1}$ captures the largest proportion of the data, $Z_{2}$ captures the next largest proportion of the variability

$V a r (Z_{1}) \geq V a r (Z_{2}) . . . \geq V a r (Z_{p})$

2 / 26

PCA (cont.)

If original variables are uncorrelated then PCA does nothing at all. The PCs are the same as the original data.
PCs are formed by calculating the eigen vectors and eigen values of the data covariance matrix.

3 / 26

Data

Rows: 344
Columns: 8
$ species           <fct> Adelie, Adelie, Adelie, Adelie, Adelie, Adelie, Adel…
$ island            <fct> Torgersen, Torgersen, Torgersen, Torgersen, Torgerse…
$ bill_length_mm    <dbl> 39.1, 39.5, 40.3, NA, 36.7, 39.3, 38.9, 39.2, 34.1, …
$ bill_depth_mm     <dbl> 18.7, 17.4, 18.0, NA, 19.3, 20.6, 17.8, 19.6, 18.1, …
$ flipper_length_mm <int> 181, 186, 195, NA, 193, 190, 181, 195, 193, 190, 186…
$ body_mass_g       <int> 3750, 3800, 3250, NA, 3450, 3650, 3625, 4675, 3475, …
$ sex               <fct> male, female, female, NA, female, male, female, male…
$ year              <int> 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007…

      species          island    bill_length_mm  bill_depth_mm  
 Adelie   :152   Biscoe   :168   Min.   :32.10   Min.   :13.10  
 Chinstrap: 68   Dream    :124   1st Qu.:39.23   1st Qu.:15.60  
 Gentoo   :124   Torgersen: 52   Median :44.45   Median :17.30  
                                 Mean   :43.92   Mean   :17.15  
                                 3rd Qu.:48.50   3rd Qu.:18.70  
                                 Max.   :59.60   Max.   :21.50  
                                 NA's   :2       NA's   :2      
 flipper_length_mm  body_mass_g       sex           year     
 Min.   :172.0     Min.   :2700   female:165   Min.   :2007  
 1st Qu.:190.0     1st Qu.:3550   male  :168   1st Qu.:2007  
 Median :197.0     Median :4050   NA's  : 11   Median :2008  
 Mean   :200.9     Mean   :4202                Mean   :2008  
 3rd Qu.:213.0     3rd Qu.:4750                3rd Qu.:2009  
 Max.   :231.0     Max.   :6300                Max.   :2009  
 NA's   :2         NA's   :2

4 / 26

Data Cleaning

# A tibble: 6 × 8
  species island culmen_length culmen_depth flipper_length body_mass sex    year
  <fct>   <fct>          <dbl>        <dbl>          <int>     <int> <fct> <int>
1 Adelie  Torge…          39.1         18.7            181      3750 male   2007
2 Adelie  Torge…          39.5         17.4            186      3800 fema…  2007
3 Adelie  Torge…          40.3         18              195      3250 fema…  2007
4 Adelie  Torge…          36.7         19.3            193      3450 fema…  2007
5 Adelie  Torge…          39.3         20.6            190      3650 male   2007
6 Adelie  Torge…          38.9         17.8            181      3625 fema…  2007

      species          island    culmen_length    culmen_depth   flipper_length
 Adelie   :146   Biscoe   :163   Min.   :32.10   Min.   :13.10   Min.   :172   
 Chinstrap: 68   Dream    :123   1st Qu.:39.50   1st Qu.:15.60   1st Qu.:190   
 Gentoo   :119   Torgersen: 47   Median :44.50   Median :17.30   Median :197   
                                 Mean   :43.99   Mean   :17.16   Mean   :201   
                                 3rd Qu.:48.60   3rd Qu.:18.70   3rd Qu.:213   
                                 Max.   :59.60   Max.   :21.50   Max.   :231   
   body_mass        sex           year     
 Min.   :2700   female:165   Min.   :2007  
 1st Qu.:3550   male  :168   1st Qu.:2007  
 Median :4050                Median :2008  
 Mean   :4207                Mean   :2008  
 3rd Qu.:4775                3rd Qu.:2009  
 Max.   :6300                Max.   :2009

5 / 26

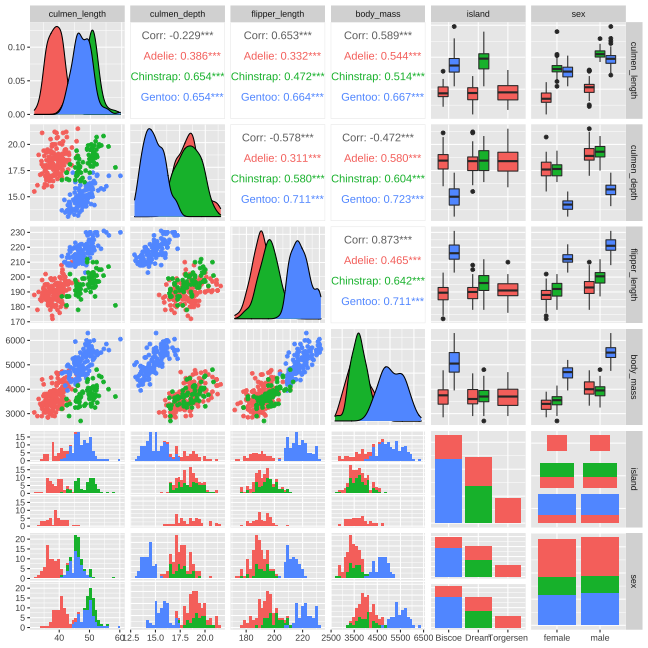
6 / 26

Artwork by @allison_horst

7 / 26

Artwork by @allison_horst

8 / 26

PCA

Select numerical variables
scale the data to 0 mean and unit variance.
Perform PCA.

9 / 26

PCA

Standard deviations (1, .., p=4):
[1] 1.6569115 0.8821095 0.6071594 0.3284579
Rotation (n x k) = (4 x 4):
                      PC1         PC2        PC3        PC4
culmen_length   0.4537532 -0.60019490 -0.6424951  0.1451695
culmen_depth   -0.3990472 -0.79616951  0.4258004 -0.1599044
flipper_length  0.5768250 -0.00578817  0.2360952 -0.7819837
body_mass       0.5496747 -0.07646366  0.5917374  0.5846861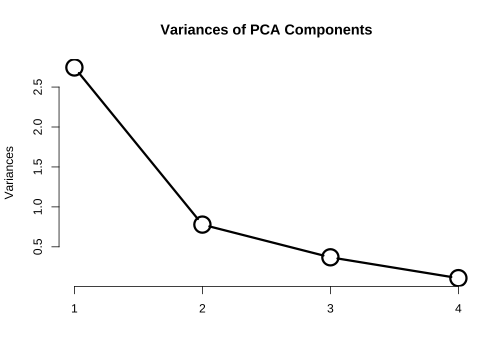

10 / 26

Standard deviations associated with PCs

summary(pca)

Importance of components:
                          PC1    PC2     PC3     PC4
Standard deviation     1.6569 0.8821 0.60716 0.32846
Proportion of Variance 0.6863 0.1945 0.09216 0.02697
Cumulative Proportion  0.6863 0.8809 0.97303 1.00000

PCA rotation matrix

pca$rotation

                      PC1         PC2        PC3        PC4
culmen_length   0.4537532 -0.60019490 -0.6424951  0.1451695
culmen_depth   -0.3990472 -0.79616951  0.4258004 -0.1599044
flipper_length  0.5768250 -0.00578817  0.2360952 -0.7819837
body_mass       0.5496747 -0.07646366  0.5917374  0.5846861

11 / 26

Predict PCs

predict(pca, newdata=tail(penguins))

            PC1         PC2        PC3         PC4
[1,] -0.4507833 -0.06535056 -0.7461058 -0.01287014
[2,]  0.5526429 -2.34408404 -0.8679388 -0.38749681
[3,] -0.7388017 -0.24778208 -0.3155918 -0.73267497
[4,] -0.3673370 -0.98959040 -0.8866618  0.19556826
[5,]  0.4916198 -1.48261810 -0.3294640 -0.55003132
[6,] -0.2130962 -1.25965815 -0.7648157 -0.10807071

tail(pca$x)

           PC1         PC2        PC3         PC4
328 -0.4507833 -0.06535056 -0.7461058 -0.01287014
329  0.5526429 -2.34408404 -0.8679388 -0.38749681
330 -0.7388017 -0.24778208 -0.3155918 -0.73267497
331 -0.3673370 -0.98959040 -0.8866618  0.19556826
332  0.4916198 -1.48261810 -0.3294640 -0.55003132
333 -0.2130962 -1.25965815 -0.7648157 -0.10807071

12 / 26

PCA

        PC1         PC2         PC3        PC4
1 -1.850808 -0.03202119  0.23454869  0.5276026
2 -1.314276  0.44286031  0.02742880  0.4011230
3 -1.374537  0.16098821 -0.18940423 -0.5278675
4 -1.882455  0.01233268  0.62792772 -0.4721826
5 -1.917096 -0.81636958  0.69999797 -0.1961213
6 -1.770356  0.36567266 -0.02841769  0.5046092

Original data

# A tibble: 6 × 8
  species island culmen_length culmen_depth flipper_length body_mass sex    year
  <fct>   <fct>          <dbl>        <dbl>          <int>     <int> <fct> <int>
1 Adelie  Torge…          39.1         18.7            181      3750 male   2007
2 Adelie  Torge…          39.5         17.4            186      3800 fema…  2007
3 Adelie  Torge…          40.3         18              195      3250 fema…  2007
4 Adelie  Torge…          36.7         19.3            193      3450 fema…  2007
5 Adelie  Torge…          39.3         20.6            190      3650 male   2007
6 Adelie  Torge…          38.9         17.8            181      3625 fema…  2007

13 / 26

Combine PCA + original data

pcadf <- data.frame(pca$x)
penguins_pca <- bind_cols(penguins, pcadf)
head(penguins_pca )

# A tibble: 6 × 12
  species island culmen_length culmen_depth flipper_length body_mass sex    year
  <fct>   <fct>          <dbl>        <dbl>          <int>     <int> <fct> <int>
1 Adelie  Torge…          39.1         18.7            181      3750 male   2007
2 Adelie  Torge…          39.5         17.4            186      3800 fema…  2007
3 Adelie  Torge…          40.3         18              195      3250 fema…  2007
4 Adelie  Torge…          36.7         19.3            193      3450 fema…  2007
5 Adelie  Torge…          39.3         20.6            190      3650 male   2007
6 Adelie  Torge…          38.9         17.8            181      3625 fema…  2007
# … with 4 more variables: PC1 <dbl>, PC2 <dbl>, PC3 <dbl>, PC4 <dbl>

14 / 26

PC1 vs PC2

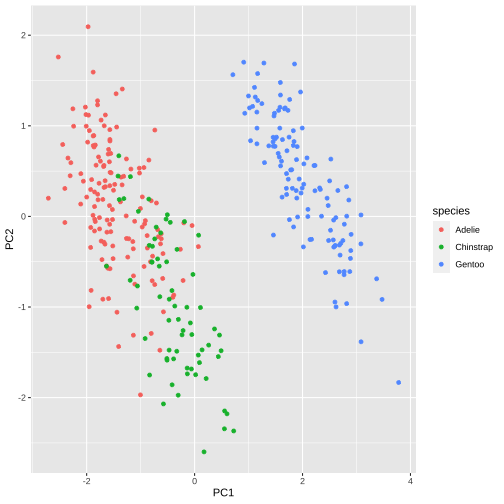
15 / 26

Plotting PCA

Standard deviations (1, .., p=4):
[1] 1.6569115 0.8821095 0.6071594 0.3284579
Rotation (n x k) = (4 x 4):
                      PC1         PC2        PC3        PC4
culmen_length   0.4537532 -0.60019490 -0.6424951  0.1451695
culmen_depth   -0.3990472 -0.79616951  0.4258004 -0.1599044
flipper_length  0.5768250 -0.00578817  0.2360952 -0.7819837
body_mass       0.5496747 -0.07646366  0.5917374  0.5846861

[1] 68.633893 19.452929  9.216063  2.697115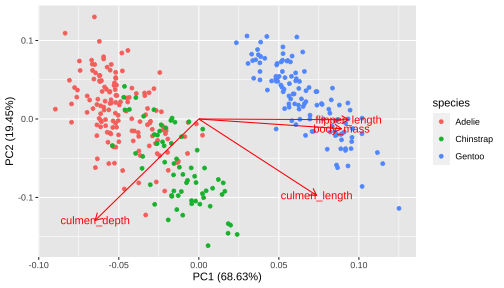

16 / 26

Biplot - plot each variables coefficients inside a unit circle

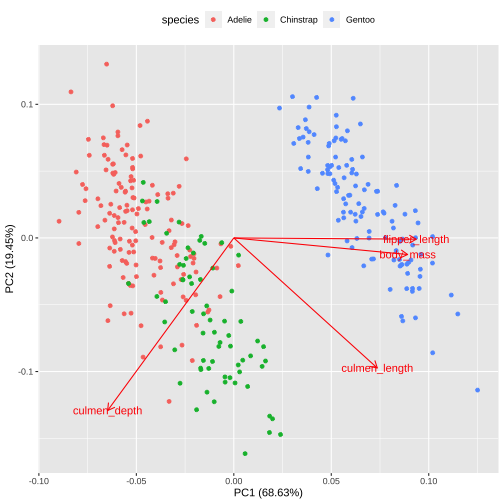
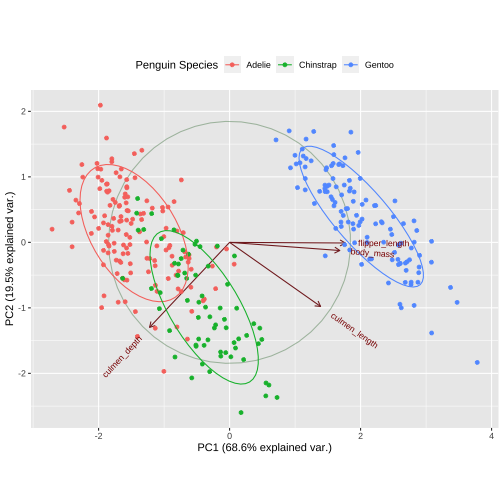
PCA rotation

                      PC1         PC2        PC3        PC4
culmen_length   0.4537532 -0.60019490 -0.6424951  0.1451695
culmen_depth   -0.3990472 -0.79616951  0.4258004 -0.1599044
flipper_length  0.5768250 -0.00578817  0.2360952 -0.7819837
body_mass       0.5496747 -0.07646366  0.5917374  0.5846861

17 / 26

Plotting PCA - PC118 / 26

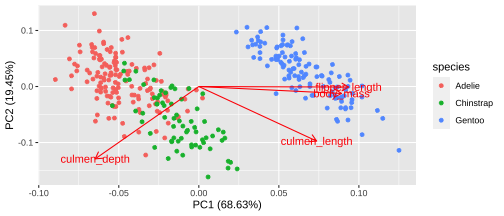
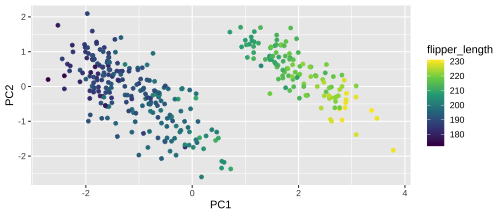
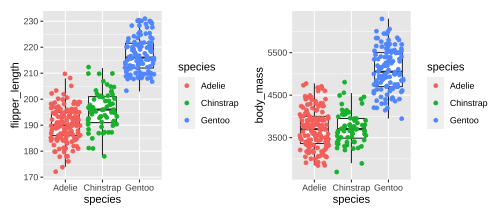
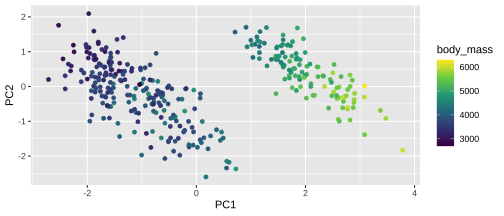
19 / 26

Plotting PCA - PC120 / 26

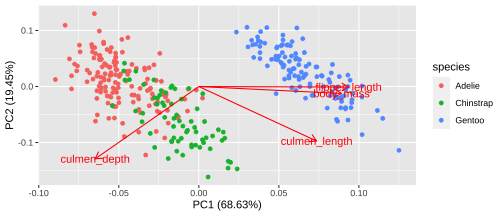
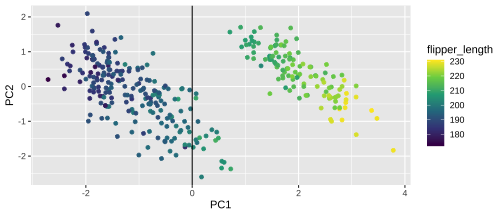
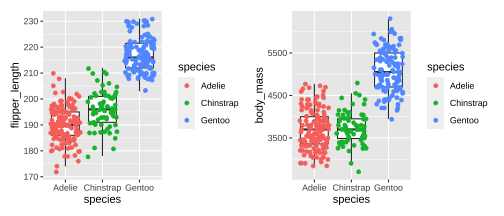
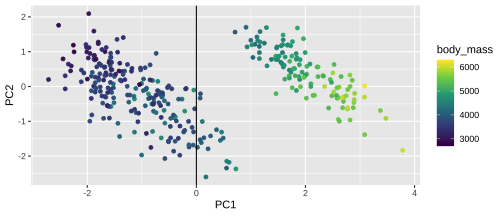
21 / 26

Plotting PCA - PC222 / 26

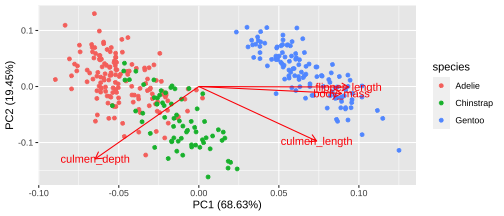
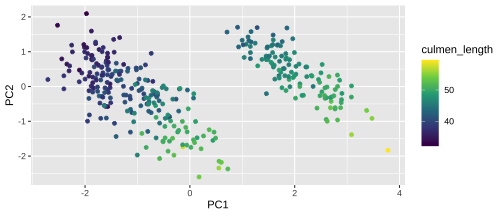
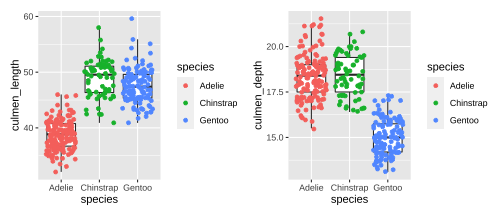
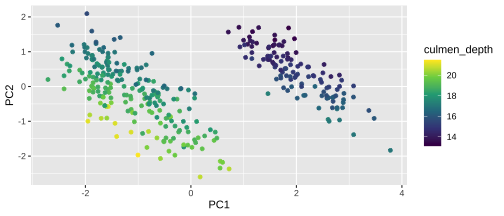
23 / 26

Plotting PCA - PC224 / 26

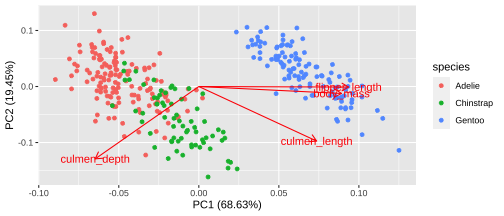
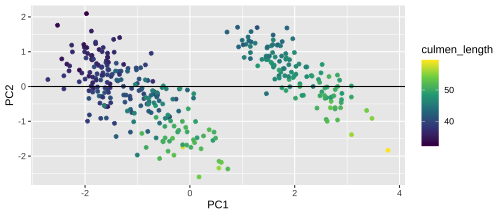
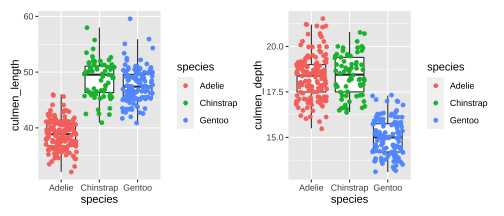
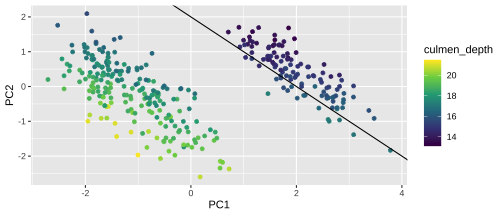
25 / 26

Visualising instance space

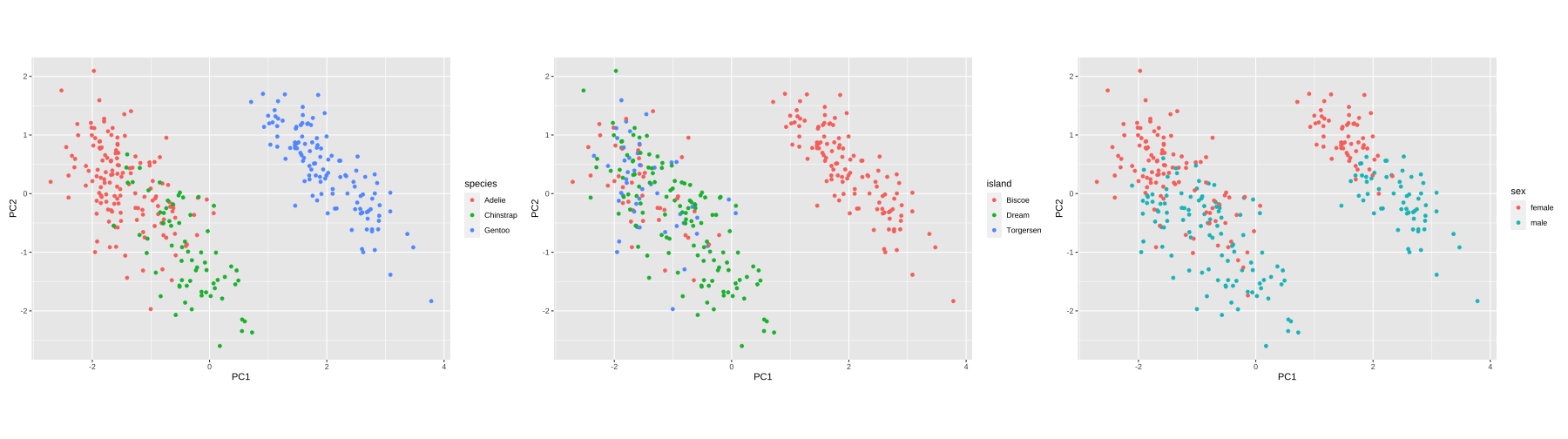
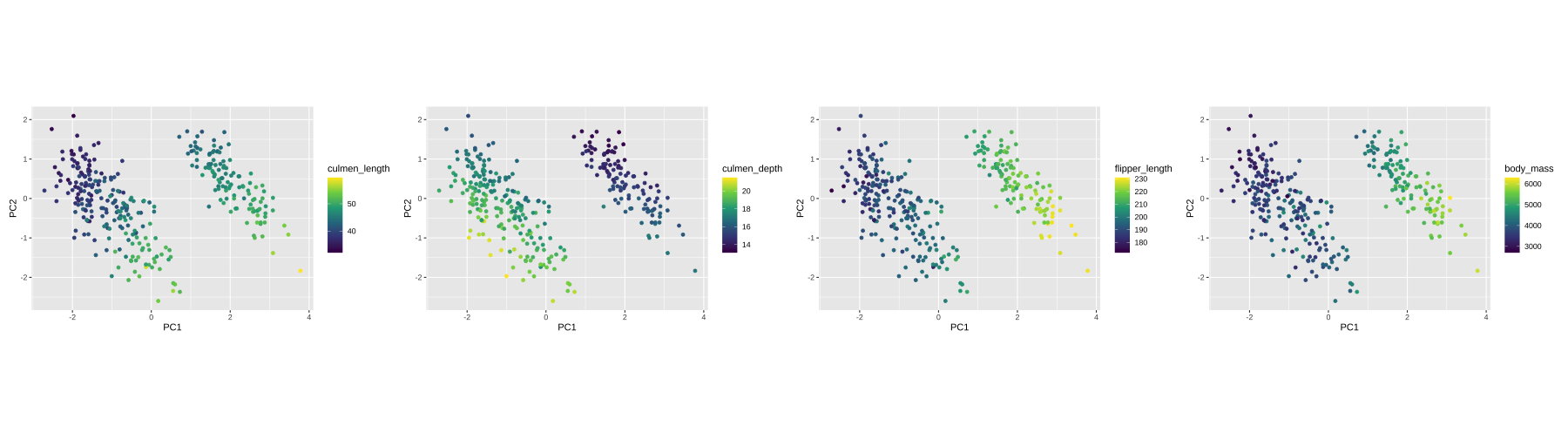
26 / 26

PCA

Finding low-dimensional combinations (or projections) of high dimensional data that capture most of the variability in the original data.

Objective: Take $P$ variables $X_{1}, X_{2}, X_{3}, . . . X_{p}$ and find combinations of these to produce variables (components) $Z_{1}, Z_{2} . . . Z_{p}$ that are uncorrelated.

Number of PCs = Number of variables in the original data.

The components are ordered so that

Z_{1}

captures the largest proportion of the data,

Z_{2}

captures the next largest proportion of the variability

$V a r (Z_{1}) \geq V a r (Z_{2}) . . . \geq V a r (Z_{p})$

2 / 26

Help

Keyboard shortcuts

↑, ←, Pg Up, k

Go to previous slide

↓, →, Pg Dn, Space, j

Go to next slide

Home

Go to first slide

End

Go to last slide

Number + Return

Go to specific slide

b / m / f

Toggle blackout / mirrored / fullscreen mode

Clone slideshow

Toggle presenter mode

Start & Stop the presentation timer

Reset the presentation timer

?, h

Toggle this help